

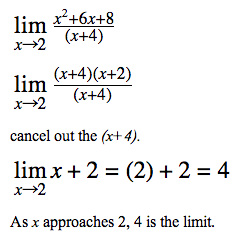
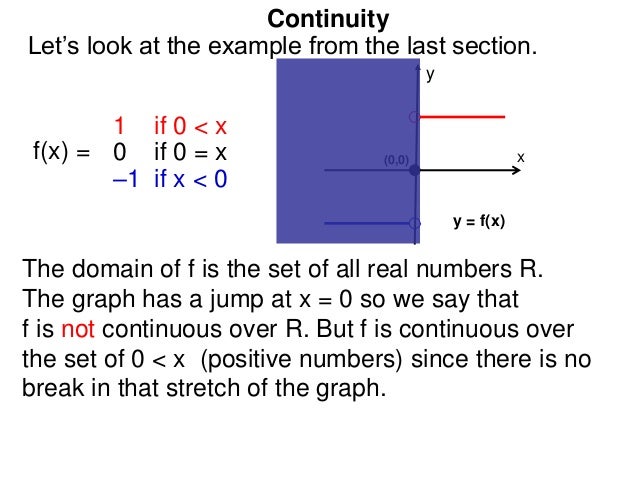
Points of continuity enjoy a type of extended continuity.' (The following lemma slightly generalizes parts of 5. Limits and Continuity, University Calculus: Early Transcendentals by Numerade. We denote the set of points of continuity of a function f : X Y between two topological spaces by C(f). I was also looking at some epsilon-delta definitions however, these seem more complicated than necessary. In this section we consider sets of points of conti-nuity for quasicontinuous functions. Explain the three conditions for continuity at a point. Is there another definition I can easily apply to prove continuity. Name AP Calculus AB Chapter 2 Day 4 2.3 Continuity Continuous Extension Function of f(x) : A function. This product is protected by copyright and distributed under licenses restricting its use, copying, distribution, and decompilation.& \frac$ is continuous if $g(x)\neq0\forall x$ however, I am hindered by the fact that $x$ intersects the x-axis (and is equal to 0 at $x=0$), or am I misinterpreting this definition for continuity? from MATH AP Calculu at Darien High School. © Maplesoft, a division of Waterloo Maple Inc., 2023. The function f x is said to be continuous at the point x = a if, for every &varepsilon > 0 there is a &delta &varepsilon for which &verbar x − a &verbar > For example the characteristic function of ( a, b), ( a, b): R R, is continuous in ( a, b) but discontinuous at a and b. Given: f(x) 11x 1 x f ( x) 11 x 1 x what should the extended function's value (s) be so that the function is continuous from the right and left Am I supposed to find the left-hand and right-hand limits and equate them to calculate the answer I'm still in Calculus 1 so the L'Hopital rule doesn't apply yet. Since a, b ( a, b), we can have a discontinuity there. This is the notion that the formal definition below captures in mathematical language. 4 Answers Sorted by: 3 As you stated in the definition, f: X Y is continuous on ( a, b) X if it is continuous at every point of ( a, b). In other words, small changes imply small changes. The above results can be easily extended in case of more than two functions.
It relies on more advanced mathematics, though, so we will wait before introducing it. Such problems arise in calculus and geometry. However, f x = x 2 sin 1 / x can't be drawn through the point x = 0 because of the infinite oscillations, but it turns out to be "continuous." The essence of this section is a rigorous concept of "continuity" at a point, and on an interval.Ī function f is continuous at x = a is small changes in x in the vicinity of a result in small changes in the values of f. Limit and Continuity function f (x) as x. We can extend the definition of continuity to closed intervals by. An extension operator preserving the modulus of continuity of a function is proposed and its. For example, at one time it was naively thought that a continuous function was one whose graph could be drawn without taking pencil from paper.
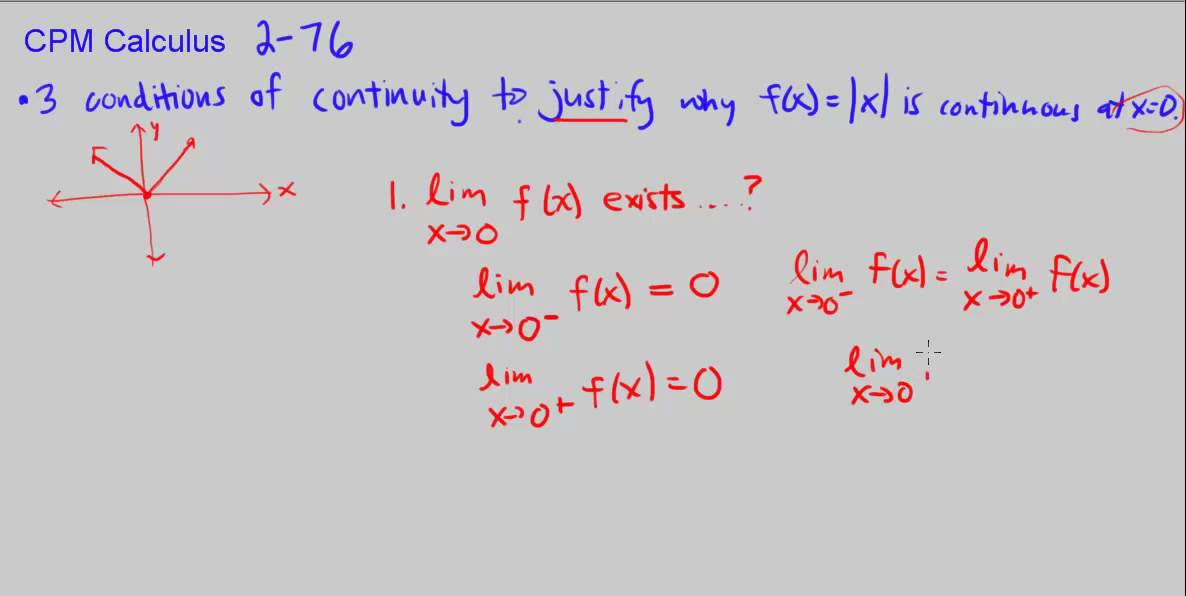
lim x a + f(x) f(a) and lim x b f(x) f(b). Note that the last two condition are equivalent to. f(x) is continuous on (a, b), f(x) is continuous from the right at a, and. During this time, the notion of "continuity" was also being articulated as the analytic property of a function that reflected any "smoothness" in its graph. A function f(x) is continuous on the closed interval a, b when. In the years after Newton and Leibniz promulgated the calculus, a rigorous definition of the limit was evolving.


 0 kommentar(er)
0 kommentar(er)
